Der Zauberspruch („Zehner mit Zehner und Einer mit Einer“)

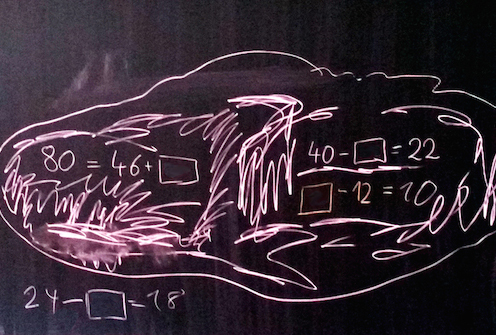
Dieses Tafelbild stammt von der letzten Diagnose-Sitzung. Karla, Ende zweiter Klasse, bekam hier den Auftrag die leeren Kästchen mit den richtigen Zahlen zu füllen. Spontan kreiste sie zunächst drei der vier Aufgaben in einer Wolke ein.
Karla war in der Schule auffällig geworden, weil sie im Fach Mathematik zunehmend schwerfällig agiert und ihre Ergebnisse für den Außenstehenden immer unverständlicher wurden, seit der Zahlenraum bis 100 erschlossen wurde. Die Lehrerin legte den Eltern schließlich nahe, Karla auf Dyskalkulie testen zu lassen. Dazu dienen beispielsweise die sogenannten Standard-Tests, die fast ausschließlich quantitativ ausgelegt sind, was bedeutet, dass die der Jahrgangsstufe angepassten mathematischen Aufgaben im Anschluss als richtig oder falsch eingeordnet und gezählt werden. Der prozentuale Anteil der richtigen Aufgaben ergibt letztendlich, nach einigen Korrelationen und im Abgleich mit einem Intelligenztest, ein Ja oder Nein zu Dyskalkulie. Es gibt aber auch qualitative Tests, die in einem Gesprächs-Dialog den Erwerb der mathematischen Kompetenz von Beginn an „abklopfen“ und den genauen Ausstiegspunkt aus der Mathematik, die dann entwickelte Sichtweise und die verwendeten Kompetenzstrategien aufdecken. Ich analysiere in meiner Praxis qualitativ, beruhend auf Michael Wehrmanns „Qualitative Diagnostik von Rechenschwierigkeiten“ (ISBN 3-89574-474-3), neben dem AFS-Test zur Ermittlung der Ursachen für den mathematischen „Ausstieg“.
Karlas Konzentration war in der bisherigen Sitzung bereits stark strapaziert worden und so war es für sie eine willkommene Abwechslung, dass sie die nächsten Aufgaben an der Tafel lösen sollte. Verhaltensbeobachtung und vor allem der Dialog mit dem Kind sind in der qualitativen Diagnose weit wichtiger, als die Richtigkeit der produzierten Ergebnisse und so fragte ich zunächst nach dem Zweck der Wolke, mit der sie 3 Aufgaben eingekreist hatte. „Die Aufgaben sind schwer“, erläuterte sie, “und die eine ist leicht“.
Kinder mit Rechenschwierigkeiten behandeln die Mathematik in den seltensten Fällen, als das was es ist, nämlich als Abbildung eines realen Sachverhaltes, der mit einer Geschichte schnell zu umschreiben wäre. Für sie ist Mathematik ein Zauberwerk, beruhend auf einer immer länger werdenden Reihe von Zahlen, dem „Zahlenalphabeth“, an dem man rauf und runter zählt. Geht es mit dem Zählen nicht mehr, dann gibt es viele verschiedene „Zauberformeln“, die man alle auswendig wissen muss, den sogenannten „Tricks“, aus denen man dann genau die richtige für die Lösung herausfischen muss.
Karla hatte in ihrem Auftrag an der Tafel offensichtlich zwei verschiedene Anforderungen identifiziert, die in der Wolke und die andere „leichte“. Für den erfahrenen Diagnostiker erglüht hier bereits ein Hoffnungsschimmer, denn mit hoher Wahrscheinlichkeit hat Karla in der Aufgabe „24 minus ?=18“ die kardinale Nähe der Zahlen 24 und 18 erfasst. Auch wenn sie die beiden Zahlen nicht als fast gleichgroße Mengen visualisiert, dann zumindest als „Fast-Nachbar“ im Zahlenalphabeth. Das bedeutet für Karla: Zauberformel „Zählen“ abrufen. Das ist ihrer Meinung nach leicht. Sie ermittelte als passende Zahl „7“. Das hatte ich erwartet, auch wenn 6 richtiger gewesen wäre. Mit der 7 bestätigte sie mir, ohne dass ich nachfragen müsste, dass sie gezählt hatte. Bei den zählenden Kindern kommt es überaus häufig vor, dass sie die Ausgangszahl mitzählen (s. auch meinen Artikel „Ich weiß jetzt, wie ihr rechnet!“) und so hatte Karla mit „24, 23, 22, 21, 20, 19, 18“ sieben Schritte ermittelt – ihr Ergebnis.
Diese Aufgabe mochte sie und es wurde ein Herzchen ergänzt. Die anderen Aufgaben waren für sie „Try & Error“ und daher benötigte sie dafür lange Zeit. Da Karla keine Mengenvorstellung mit der Mathematik verbindet, kann sie auch nicht die gesuchten Zahlen durch Umkehr-Aufgaben herleiten. Ihr bleibt nur das Ausprobieren, solange bis der resultierende Term für sie richtig ausschaut. Für solche zweistelligen komplizierten Aufgaben hatte sie einen anderen „Trick“. Eine Zauberformel, die ihr die Großmutter beim Matheüben verraten hat. „Rechne: Zehner mit Zehner und dann Einer mit Einer“, hatte die Oma ihr mit auf den Weg gegeben und diesen Zauberspruch wendete sie immer bei solchen Aufgaben unverstanden an. Karla probierte bei den Aufgaben verschiedene Lösungen aus, bis der „Trick“ passte. Nebenbei bemerkt war das ein Vorgang, der höchste Intelligenz erfordert, denn, was ich ihnen hier nicht vermitteln kann, ist die Einschachtelungsmethode, mit der sie ihre Lösungsversuche immer weiter eingrenzte. Es war keineswegs so, dass sie Zahl für Zahl durchprobierte. Sie steuerte mit ihren Versuchen zielstrebig auf die letztendlich gefundenen Zahlen zu, die sie auch nach nochmaliger Kontrolle für absolut richtig hält.
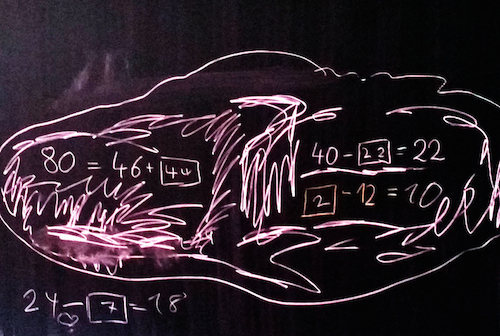
„80 = 46+44, denn 4 Zehner und 4 Zehner sind 8 Zehner und wenn ich 6 Einer und 4 Einer zusammenzähle, dann habe ich 10, das sind wieder 0 Einer.“ Der Term stimmt für Karla und damit auch die Lösung 44.
„40-22=22, denn 4 Zehner minus 2 Zehner sind 2 Zehner, 0-2 geht nicht, also rechne ich 2-0 und das sind 2 Einer. “ Wieder stimmt für Karla der Term, also auch die gefundene 22.
„2-12=10, 0 Zehner minus 1 Zehner geht nicht, also rechne ich 1-0, das sind 1 Zehner und 2 Einer minus 2 Einer sind 0 Einer.“
Der Term stimmt für Karla abermals und damit auch ihre gefundene Lösung 2. Sie war mit Recht stolz auf ihre Leistung. Zur Vermeidung von Frust bewerte ich in der Diagnose nicht das Ergebnis und verrate auch nicht, ob es richtig oder falsch ist. Wichtig ist die Erkenntnis: Es mangelt Karla nicht an Intelligenz, nicht an logischem Geschick und nicht am Ehrgeiz. Sie hat die Mathematik missverstanden und sieht leider keinen Zusammenhang mit dem Alltag, aber das lässt sich in einer Therapie durch den Neuaufbau der mathematischen Kompetenz erreichen. Dann wird das Zauberwerk zu einem verstandenen Vorgang und das Rechnen macht wieder Spaß. (FH)
Text und Bilder: Frank Haub
Wir freuen uns sehr, dass Frank Haub aus Remagen sich bereit erklärt hat, öfters aus seiner Praxis zu berichten. Wir haben Herrn Haub auf der Fachtagung des EÖDL kennengelernt, wo er einen Vortrag über “Effiziente Didaktik für das Symptomtraining dyskalkuler Kinder” hielt. Herr Haub ist Diplom-Informatiker und Diplomierter Dyskalkulietrainer. Er hat eine Praxis in Remagen, wo er dyskalkule Kinder unterstützt. Frank Haub bietet auch Vorträge zum Thema Dyskalkulie an sowie Fortbildungen für Lehrkräfte. Weitere Informationen finden Sie auf seiner Internetseite: www.dys-remagen.de
Lesen Sie auch:



[…] Der Zauberspruch („Zehner mit Zehner und Einer mit Einer“) […]